Метод динамічного програмування та його особливості 🧩

Якщо ви коли-небудь стикалися із завданнями, де потрібно визначити найкраще рішення на основі певного набору обмежень, то ви, ймовірно, знаєте, що існує для цього метод динамічного програмування. Це досить потужний апарат, і за його допомогою можна розв’язувати задачі різної складності, від пошуку найбільшої загальної підпослідовності до визначення найвигіднішої комбінації товарів для рюкзака. Якщо ви хочете навчитися застосовувати цей метод, то вам необхідно розуміти, як працює апарат динамічного програмування. Усі ці питання ми розглянемо в цьому матеріалі.

Опис методу

Поняття “динамічне програмування” придумав і назвав 1940 року Річард Беллман, а змінив і доповнив його визначення – 1953 року. Беллману довелося багато часу витратити на вибір назви, бо його бос не любив математичні терміни. Тому автор визначення вибрав слово “програмування” замість “планування” і слово “динамічне”, щоб уникнути принизливих і лайливих тлумачень з боку керівника. Ось так було сформовано назву “динамічне програмування”.

Метод динамічного програмування (ДП) є одним з основних інструментів оптимізації та розв’язання задач в інформатиці, економіці, біології та інших галузях. Простими словами, динамічне програмування – це метод розв’язання задач, що ґрунтується на розбитті складної задачі на безліч дрібніших;

Важливо враховувати такі моменти:

Для ефективного застосування цього підходу необхідно запам’ятовувати рішення підзадач.
Підзадачі мають загальну структуру, що дає змогу використовувати однорідний спосіб їх розв’язання, замість того, щоб кожну вирішувати окремо різними алгоритмами.

Навіщо він потрібен

За допомогою ДП ефективно розв’язують задачі з оптимізації, наприклад, якщо потрібно знайти найбільше або найменше значення функції. ДП також активно застосовується в задачах планування, де потрібно визначити оптимальну послідовність дій.

Ознайомитися з курсами

Основні поняття

Давайте розберемося детальніше в основних поняттях методу.

Одне з головних понять – це оптимальна підструктура. Що ж це таке? У методі динамічного програмування ми розв’язуємо задачу, розбиваючи її на більш дрібні. Оптимальна підструктура означає, що найкраще рішення ми можемо отримати, якщо знаємо оптимальні рішення кожної з підзадач.

Інше важливе поняття – підзадачі, що перекриваються. Тут ми можемо зіткнутися з ситуацією, коли різні підзадачі мають спільні частини. У такому разі кажуть, що в нас є підзадачі, які перекриваються. Щоб не розв’язувати одну й ту саму задачу безліч разів, ми зберігаємо результати підзадач у пам’яті та перевикористовуємо їх під час розв’язання більших завдань. Це допомагає значно прискорити процес розв’язання.

Наприклад, нехай у нас є задача про знаходження найбільшої загальної підпослідовності двох рядків. Ми можемо розв’язувати її методом динамічного програмування, розбивши її на більш дрібні підзадачі – знаходження загальної підпослідовності для підрядків кожного з рядків. У цьому разі ми стикаємося з підзадачами, що перекриваються, – загальна підпослідовність для деяких підрядків уже може бути розрахована раніше і збережена в пам’яті. Таким чином, ми можемо уникнути повторних обчислень і розв’язати задачу більш ефективно.

ДП – це методологія розв’язання задач, яка являє собою не просто формулу або алгоритм, це скоріше роздуми про те, як розв’язати задачу.

Цей підхід вимагає розбиття задачі на дрібніші, простіші підзадачі (із вхідними даними меншого розміру, як-от менша кількість, масив меншого розміру або менша кількість параметрів, які можна налаштувати).
Розв’язки дрібніших підзадач можуть бути використані для розв’язання великої вихідної задачі. Прикладом може слугувати обчислення чисел Фібоначчі.
При цьому важливо ефективно використовувати розв’язки підзадач, наприклад, запам’ятовуючи їх, а також використовувати однорідний спосіб розв’язання для всіх підзадач, якщо вони мають спільну структуру.

Алгоритм методу динамічного програмування

Алгоритм методу динамічного програмування складається з кількох кроків:

Визначення структури оптимізаційної задачі. Необхідно визначити, які параметри задачі є змінними, які є константами, які обмеження існують на змінні.
Формулювання рекурсивної формули. Необхідно виразити розв’язання задачі через розв’язання дрібніших підзадач. Рекурсивна формула має бути коректною і мати властивість оптимальної підструктури.
Створення таблиці для зберігання результатів підзадач. Необхідно створити таблицю, де в кожній комірці зберігатиметься оптимальне розв’язання для відповідної підзадачі.
Заповнення таблиці. Необхідно заповнити таблицю, починаючи з найменших підзадач і поступово переходячи до більших. Під час заповнення таблиці використовується рекурсивна формула.
Отримання розв’язку вихідної задачі. Розв’язок вихідної задачі міститься в останній комірці таблиці.

Алгоритм методу ДП може бути застосований до широкого спектра задач, включно із задачами знаходження найкоротшого шляху в графі, оптимального розкладу робіт, знаходження максимального потоку в мережі та інші. Він має низку переваг, але також має недоліки і вимагає досить великого обсягу пам’яті для зберігання результатів підзадач.

Приклади застосування методу

Розглянемо два приклади застосування цієї техніки програмування.

Числа Фібоначчі

Одним із найвідоміших прикладів використання методу динамічного програмування може бути розрахунок чисел Фібоначчі. Для обчислення будь-якого числа в послідовності нам необхідно спочатку обчислити два попередніх числа і скласти їх. Таким чином, для обчислення кожного наступного числа ми використовуємо результати попередніх обчислень. Хоча для обчислення чисел Фібоначчі є і замкнута формула.

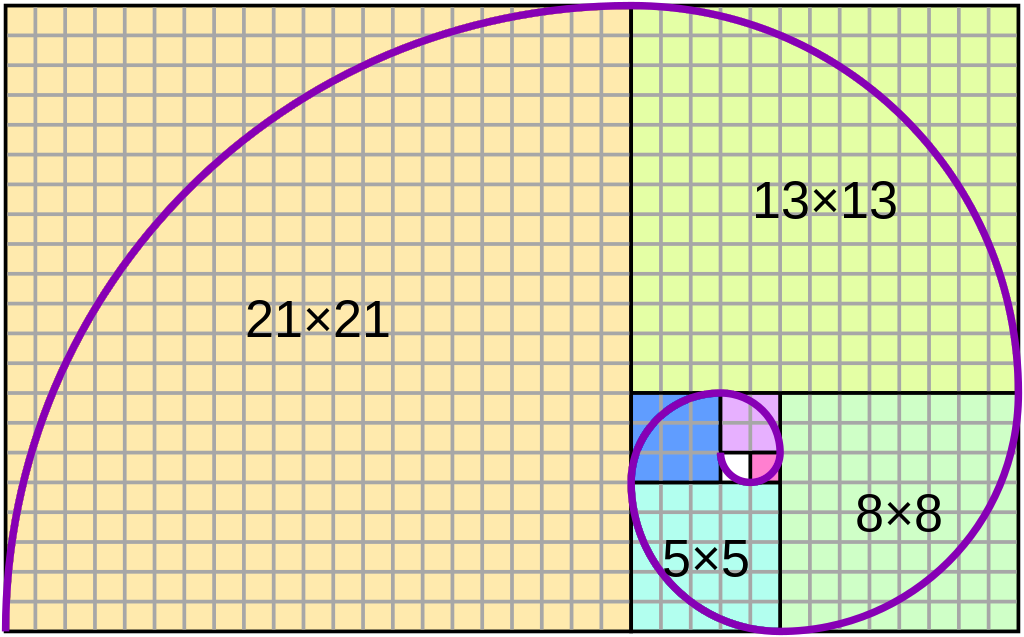
Нехай у вас є набір чисел, і вам потрібно знайти максимальну суму, яку можна отримати, вибравши деякі з них, за умови, що вибрані числа не повинні стояти поруч одне з одним. Наприклад, для набору чисел [1, 2, 3, 1] максимальна сума дорівнює 4 (виберіть числа 1 і 3).

Це може здатися складним, але такий підхід дає змогу розв’язувати задачі в оптимальний спосіб і часто використовується в алгоритмах оброблення зображень, оброблення природної мови, ігрових додатках та інших галузях.

Візьмемо практичний приклад мовою Python:

def max_sum_sequence(nums):

n = len(nums)

if n == 0:

return 0

if n == 1:

return nums[0]

# Обчислюємо максимальну суму для кожного елемента

dp = [0] * n

dp[0] = nums[0]

dp[1] = max(nums[0], nums[1])

for i in range(2, n):

dp[i] = max(dp[i-1], dp[i-2] + nums[i])

# Повертаємо максимальну суму для останнього елемента

return dp[-1]

Функція max_sum_sequence приймає список nums, що містить числа, і повертає максимальну суму підпослідовності. Спочатку ми перевіряємо довжину списку, якщо він порожній, то повертаємо 0, а якщо він містить тільки один елемент, то повертаємо його значення. Потім ми створюємо масив dp, в якому будемо зберігати максимальну суму для кожного елемента списку. Для першого елемента максимальна сума дорівнює самому елементу, а для другого елемента максимальна сума дорівнює максимальному значенню з двох перших елементів. Далі ми перебираємо елементи списку, що залишилися, і для кожного елемента обчислюємо максимальну суму, яку можна отримати, якщо вибрати елементи тільки з цього елемента і всіх елементів, що передують йому, але не з його сусідів. Для цього ми використовуємо формулу dp[i] = max(dp[i-1], dp[i-2] + nums[i]), де dp[i-1] – максимальна сума до попереднього елемента, а dp[i-2] + nums[i] – максимальна сума до поточного елемента, якщо ми не вибрали попередній елемент. Нарешті, ми повертаємо максимальну суму для останнього елемента списку, що і дає нам відповідь на вихідну задачу.

Вартість рюкзака

Ще одним прикладом використання методу ДП може бути розрахунок вартості рюкзака;

Припустімо, у вас є рюкзак і набір предметів із певними вагами та вартостями. Вам потрібно заповнити рюкзак таким чином, щоб максимізувати вартість обраних предметів, не перевищуючи місткість рюкзака.

Для розв’язання цієї задачі ми можемо використовувати таблицю заповнення. У кожній комірці таблиці зберігатиметься максимальна вартість, яку ми можемо отримати, використовуючи тільки перші i предметів і маючи рюкзак місткості не більше j.

Формула для заповнення таблиці матиме такий вигляд:

f[i][j] = max(f[i-1][j], f[i-1][j-w[i]] + v[i])

де f[i][j] – максимальна вартість, яку можна отримати серед перших i предметів, використовуючи рюкзак місткості не більше ніж j, w[i] і v[i] – вага і вартість i-го предмета.

Суть цієї формули полягає в тому, що для кожного предмета ми можемо розв’язати дві підзадачі: додати його до рюкзака чи не додавати. Якщо ми не додаємо предмет, то максимальна вартість дорівнюватиме максимальній вартості серед перших i-1 предметів і рюкзака місткості j. Якщо ми додаємо предмет, то максимальна вартість дорівнюватиме сумі вартості цього предмета і максимальної вартості серед перших i-1 предметів і рюкзака місткості j-вагу[i].

У результаті заповнення таблиці, відповіддю на вихідну задачу буде максимальна вартість серед перших n предметів і рюкзака місткості не більше W, де n – кількість предметів, W – місткість рюкзака.

Наприклад, для набору предметів із вагами [3, 4, 5] і вартістю [4, 5, 6] та рюкзака місткістю 8, таблиця заповнення матиме такий вигляд:

w\j	1	2	3	4	5	6	7	8
0	0	0	0	0	0	0	0	0
3	0	0	4	4	4

Максимальна вартість рюкзака для цього набору предметів і місткості 8 дорівнює 9.

Усі ці приклади демонструють ефективність і універсальність методу ДП у розв’язанні різних завдань;

Переваги та недоліки

Як і будь-який інший алгоритм, метод він має свої переваги та недоліки. Розглянемо їх детальніше.

Переваги:

Ефективність: ДП може бути дуже ефективним для розв’язання задач, які можна розбити на підзадачі, і де оптимальне розв’язання кожної підзадачі може бути обчислено тільки один раз.

Гнучкість: може бути застосований до широкого спектра завдань (знаходження найкоротшого шляху в графі, завдання оптимального розкладу і багато інших).

Точність: на відміну від алгоритмів, які приймають локально оптимальні рішення, ДП може гарантувати глобально оптимальне рішення.

Недоліки:

Висока складність: ДП може мати високу обчислювальну складність, особливо якщо вихідна задача дуже складна і може бути розбита на безліч підзадач.

Потреба у великому обсязі пам’яті: необхідно зберігати в пам’яті значення для всіх підзадач, що може призвести до великого споживання пам’яті.

Необхідність певної структури задачі: ДП може бути неефективним або незастосовним, якщо вихідну задачу не розбити на підзадачі або якщо їхні розв’язки неможливо ефективно комбінувати для отримання розв’язку вихідної.

Підсумок

У майбутньому метод динамічного програмування продовжуватиме використовуватися в різних галузях, як-от фінанси, виробництво, транспорт і багатьох інших, для розв’язання складних завдань оптимізації. Однак, необхідно продовжувати дослідження в галузі розроблення нових алгоритмів, які будуть більш ефективні та універсальні для вирішення різних завдань.

🚀 Метод динамічного програмування: ключові аспекти та застосування