В чем важность бинарного дерева в программировании

Бинарное дерево — это структура данных, где каждый узел может иметь до двух потомков: левого и правого. Оно обеспечивает эффективное хранение и организацию данных, а также упрощает реализацию алгоритмов и операций. Исторически, бинарные деревья были разработаны для эффективного поиска и организации информации, начиная с создания бинарного поискового дерева в 1950-х годах. С течением времени они стали широко применяться в базах данных, компиляторах, алгоритмах сортировки и поиска, компьютерной графике и других областях информатики (данная тема изучается на практике на курсе Алгоритмы и структуры данных от компании FoxmindED).

В настоящее время бинарные (двоичные) деревья остаются одной из ключевых структур данных в информатике, играя важную роль в разработке программного обеспечения и решении различных задач.

Структура 

Бинарное дерево состоит из узлов, каждый из которых содержит некоторые данные и ссылки на его потомков:

• Узлы:

• ячейки памяти, хранящие данные (числа, строки, объекты);
• могут иметь ссылки на другие узлы.

• Корень:

• верхний узел дерева, не имеющий «родителя»;
• от него начинается обход дерева.

• Потомки:

• «дети» узла, на которые он ссылается;
• левый потомок всегда меньше или равен своему «родителю»;
• правый потомок всегда больше или равен своему «родителю».

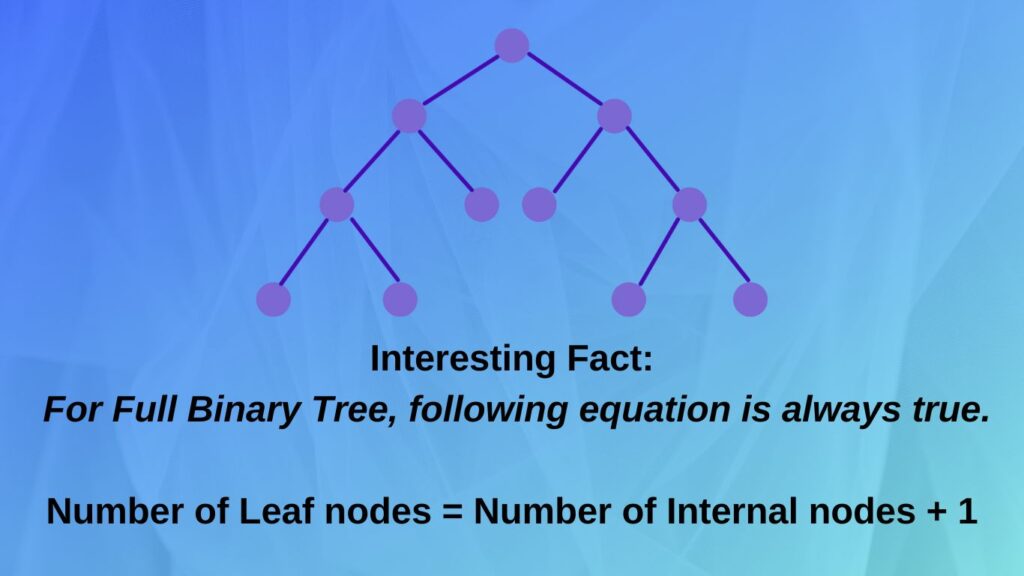
Для наглядности представим простое бинарное дерево:

       8

      /  \

     3   10

    / \       \

   1   6    14

       /  \     /

     4   7 13

Принцип работы 

Основная идея работы двоичного дерева заключается в эффективной организации и хранении данных для выполнения операций, таких как поиск, вставка, удаление и обход элементов.

Деревья работают на основе рекурсивных алгоритмов. Для операций над деревом, таких как поиск, вставка и удаление, применяются рекурсивные функции, которые обрабатывают каждый узел и его потомков.

Бинарные деревья применяются в различных областях программирования и информатики. Это и базы данных, и алгоритмы сортировки и поиска, и структуры данных.

Типы 

Существует несколько типов двоичных деревьев:

• Бинарные деревья поиска (BST): данные упорядочены так, что элементы в левом поддереве меньше значения узла, а в правом — больше. Часто используются для быстрого поиска элементов в базах данных.
• АВЛ-деревья: это специальный тип BST, где высота поддеревьев каждого узла отличается не более чем на единицу. Предотвращают деградацию производительности при больших объемах данных.
• Красно-черные деревья: еще один тип самобалансирующихся BST. Узлы дополнительно помечены красным или черным цветом. Широко используются в реализации множеств и словарей.
• Есть и другие типы, такие как B-деревья, B+ деревья, Splay-деревья и др., каждый со своими характеристиками и применением в информатике.

Приведем примеры создания бинарных деревьев на Python, Java и C++:

1. Бинарное дерево с ++

int main() {

    TreeNode* root = new TreeNode(1);

    root->left = new TreeNode(2);

    root->right = new TreeNode(3);

    root->left->left = new TreeNode(4);

    root->left->right = new TreeNode(5);

    return 0;

}

2. Бинарное дерево java

public class Main {

    public static void main(String[] args) {

        TreeNode root = new TreeNode(1);

        root.left = new TreeNode(2);

        root.right = new TreeNode(3);

        root.left.left = new TreeNode(4);

        root.left.right = new TreeNode(5);

    }

}

3. Бинарное дерево python

root = TreeNode(1)

root.left = TreeNode(2)

root.right = TreeNode(3)

root.left.left = TreeNode(4)

root.left.right = TreeNode(5)

Применение 

Бинарные деревья находят широкое применение в реальных проектах и задачах. 

• Базы данных: используются для организации индексов и быстрого поиска данных. Например, B-деревья для реляционных баз данных и B+ деревья для кластерных индексов.

• Алгоритмы поиска и сортировки: применяются в алгоритмах бинарного поиска и сортировки, таких как сортировка слиянием. 

• Реальные проекты: используются в СУБД (MySQL, PostgreSQL), поисковых системах, файловых системах (NTFS), компиляторах и интерпретаторах для анализа и хранения программного кода.

Бинарные деревья обеспечивают эффективную организацию и обработку данных, что делает их важным инструментом в различных областях информатики и программирования.

Алгоритмы 

Бинарные деревья поддерживают различные операции, такие как поиск, вставка и удаление узлов, а также обход дерева для доступа к каждому узлу в определенном порядке.

Рассмотрим порядок:

• Поиск узла: сравниваем ключи и спускаемся по дереву: влево, если ключ меньше текущего узла, вправо, если больше. Процесс повторяется до нахождения узла или достижения конца дерева.
• Вставка узла: сравниваем ключи и вставляем узел в дерево, учитывая правила порядка.
• Удаление узла: сложный процесс, включающий различные случаи в зависимости от наличия потомков у удаляемого узла.
• Обход бинарного дерева: позволяет посетить каждый узел в определенном порядке: прямой, pre-order traversal (посещение корня, затем поддеревьев), обратный, post-order traversal (посещение поддеревьев, затем корня), симметричный, in-order traversal (посещение левого поддерева, затем корня, затем правого поддерева). Используется для вывода отсортированных данных или выполнения операций над деревом.

Балансировка 

Балансировка двоичных деревьев — это процесс поддержания равновесия в структуре дерева путем перераспределения узлов. Она предотвращает деградацию производительности и увеличение времени выполнения операций при последовательных вставках и удалениях узлов.

Зачем она нужна? Без нее деревья могут стать несбалансированными, что приводит к ухудшению производительности операций из-за увеличения высоты дерева и линейной зависимости времени выполнения от количества узлов.

Алгоритмы балансировки:

• АВЛ-деревья: гарантируют баланс, поддерживая разницу высот поддеревьев каждого узла не более чем на единицу. Используют повороты и перебалансировку поддеревьев при вставке и удалении.
• Красно-черные деревья: самобалансирующиеся деревья, где каждый узел помечен красным или черным цветом. Гарантируют равное количество черных узлов на пути от корня до листов.
• Splay-деревья: перемещают часто используемые узлы ближе к корню, что обеспечивает хорошую производительность в среднем случае.

Приведем примеры алгоритмов балансировки бинарных деревьев:

• Балансировка АВЛ

• Основана на поворотах узлов для поддержания баланса.
• При вставке или удалении узла производятся повороты для выравнивания высоты поддеревьев.

• Балансировка красно-черного дерева

• Использует правила окрашивания узлов и повороты для сбалансированности.
• При изменениях в дереве производятся перекраски и повороты для поддержания баланса.

FoxmindEd — это учебный центр с большим выбором направлений курсов для новичков и программистов с опытом!

Начинаете свой путь в IТ? Попробуйте курсы Start

Имеете базовые навыки программирования? Тогда вам на курсы Junior

Хотите углубить свои знания в IТ? У нас есть курсы Middle/Senior

• Балансировка 2-3 дерева

• Основана на слиянии и разделении узлов для поддержания оптимальной структуры.
• При необходимости узлы объединяются или разделяются для сохранения баланса.

Сложность операций 

Проведем анализ временной и пространственной сложности операций в бинарных деревьях:

• Поиск узла: в сбалансированных деревьях, таких как АВЛ-деревья или красно-черные деревья, время поиска составляет O(log n), где n — количество узлов в дереве. В несбалансированных деревьях, таких как деревья поиска в худшем случае, время поиска может составлять O(n).
• Вставка узла: в сбалансированных деревьях время вставки составляет O(log n), в то время как в несбалансированных — O(n).
• Удаление узла: в сбалансированных — время составляет O(log n), в то время как в несбалансированных — O(n).
• Пространственная сложность: обычно составляет O(n), где n — количество узлов в дереве, из-за необходимости хранения данных и указателей на потомков для каждого узла.

Сравним эффективность разных типов бинарных деревьев:

• АВЛ-деревья: гарантируют логарифмическое время выполнения операций вставки, поиска и удаления, но требуют больше операций для балансировки.
• Красно-черные деревья: требуют меньше операций для балансировки и могут быть эффективнее в некоторых сценариях.
• Splay-деревья: обеспечивают хорошую производительность в среднем случае, но могут иметь неоптимальное время выполнения в худшем случае для некоторых операций.

Практические примеры и задачи

Предлагаем краткий разбор практической задачи:

Задача: необходимо реализовать бинарное дерево поиска и выполнить операции вставки и поиска элементов.

1. Определите класс Node, представляющий узел бинарного дерева. У узла должны быть поля для хранения значения, указателей на левого и правого потомка.

2. Определите класс BinarySearchTree, в котором будут реализованы методы для вставки, поиска и других операций.

3. Метод вставки узла

• Начните с корневого узла.
• Если дерево пустое, создайте новый узел и сделайте его корнем.
• Если значение нового узла меньше значения текущего узла, рекурсивно вставьте его в левое поддерево.
• Если значение нового узла больше значения текущего узла, рекурсивно вставьте его в правое поддерево.
• Обработайте случай, когда значение уже существует в дереве.

4. Метод поиска узла

• Начните с корневого узла.
• Если значение узла равно искомому, верните узел.
• Если значение искомого узла меньше значения текущего узла, рекурсивно ищите в левом поддереве.
• Если значение искомого узла больше значения текущего узла, рекурсивно ищите в правом поддереве.
• Если узел не найден, верните None.

5. Тестирование

• Создайте экземпляр класса BinarySearchTree.
• Проверьте вставку нескольких узлов и убедитесь, что они были корректно добавлены.
• Проведите поиск нескольких значений и убедитесь, что результаты поиска верны.

6. Оптимизация (по желанию)

• Реализуйте методы удаления узла, обхода дерева и другие дополнительные функции в зависимости от требований задачи.

Чтобы потренировать навыки работы с бинарными деревьями, советуем обратить внимание на такие ресурсы: онлайн-курсы и образовательные платформы (Coursera, edX, Udacity, Codecademy, LeetCode, HackerRank), учебники и книги («Introduction to Algorithms», Кормен, Лейзерсон, Ривест, Штайн, «Algorithms», Седжвик, Уэйн), онлайн-ресурсы и платформы (GitHub, Stack Overflow), интерактивные песочницы и среды разработки (Jupyter Notebook, Google Colab, Visual Studio Code, PyCharm).

А, начать можно с онлайн-курсов Java Start, C# Start, Python Start, C++ Start на платформе FoxmindED. Консультант поможет вам выбрать оптимальный курс, исходя из ваших стремлений в данной области. 

Заключение

Бинарные деревья в программировании играют важную роль. Их важность — в эффективной организации и хранении данных, а также в широком спектре применения в различных областях. Изучение этой темы открывает перед разработчиками исключительные перспективы для создания эффективных программных решений и алгоритмов.